|
Signal processing methods like iterative numeric smoothing, discrete autocorrelation function
and discrete Fourier series/transform can be used to noise reduction. The numeric smoothing has
the property of a low-pass filter. Only high-frequent noise can be filtered by the smoothing. The
magnitude and phase spectra of a sampling signal can be calculated by a windowed discrete Fourier
series/transform (DFS). If the frequencies of the spectral components of the signal are known,
the signal can be abstracted from the sampling signal. However, one cannot easily distinguish which
frequency components result from the signal, and which frequency components come from the noise.
The time noise series is fortunately uncorrelated in the most practical cases. An uncorrelated
noise can considerably be reduced by a discrete autocorrelation function (DACF), which separates
the noise from the sampling signal. In other words the signal can be abstracted by the DACF from
the sampling signal. The autocorrelation function has the same spectral components like the signal.
Therefore, the signal frequencies can be determined by the autocorrelation function. The problem
is that the magnitudes and phases of the spectral components of the signal are changed by the DACF.
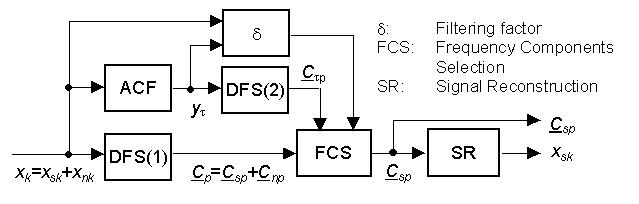
Fig. 1 Scheme of an adaptive filtering algorithm
(ACF: Autocorrelation Function, DFS: Discrete Fourier Series)
An adaptive filtering can be used to solve the problems mentioned above. Fig. 1 shows the scheme of
the algorithm based on a combination of the windowed DFS and the DACF. The sampling signal
uk is parallel processed by the DFS(1) and the DACF.
The uncorrelated noise unk is effectively filtered by the DACF.
The output signal yt is resulted mainly
from the signal usk. The spectral components C
yp of the autocorrelated signal yt
is calculated by the DFS(2) using the same time window like the DFS(1). Therefore,
the Fourier coefficients Csp of the signal usk
can be selected from the Fourier coefficients Cp of
the DFS(1) according to a defined filtering factor d. Using the coefficients
Csp one can reconstruct a time signal using the discrete Fourier
series.
For the Fourier coefficients selection (FCS) and the signal reconstruction the following relations:
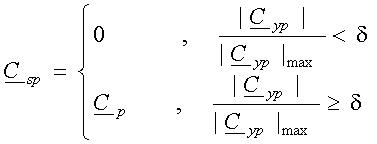
are used, where |Cyp|max is the maximum magnitude
of the Fourier coefficients Cyp and d
the filtering factor, normally, 0<d<1. The filtering factor can
be determined by the ratio between the original effective value of the sampling signal and the
effective value of the corresponding autocorrelated signal.
The transfer function of the adpative filtering is equal to 1 for signal components and 0 for
the noise parts. This filtering can be used for noise reduction of periodic and periodically
expended signals, the spectrum of which superimposes with the noise spectrum.
Fig. 2 show the simulation result of a sinusoid signal and a damped oscillation signal.
The both signals are mixed with strong noise. The noise parts are effectively filtered out by the adaptive
filtering.
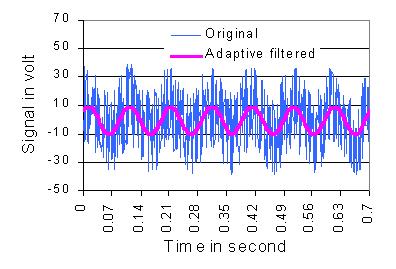
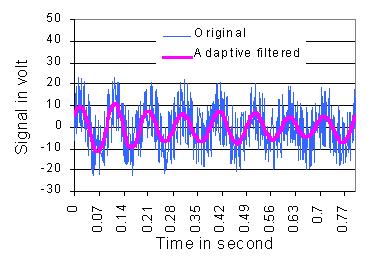
Fig. 2 Simulation results of sinusoid and oscillation signals
Fig. 3 shows the noise reduction of a dynamic strain measuring system based
fiber Bragg grating sensor . In the sensitive wavelength range, the maximal effective value of the adaptive filtered
noise is only 1/3 of the original noise. The resolution of the measuring system is improved by the
adaptive filtering. After the filtering the noise strain is less than 10-9 for the
optimized wavelength. It is much less than the original noise strain.
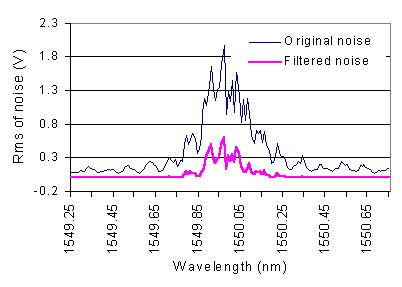
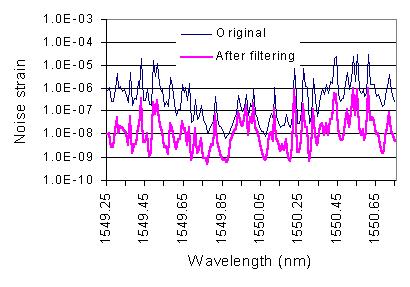
Fig. 3 Noise effektive value and noise strain of fiber Bragg grating
measuring system
Fig. 4 shows the noise reduction of a seismic signal. The original signal is generated by blast
exciting in undergroud building and detected with the fiber optic Bragg grating sensor system.
The signal is mixed with a strong noise. After the adpative filtering the noise parts are
reasonably reduced.
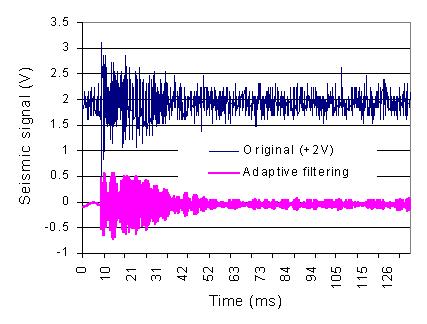
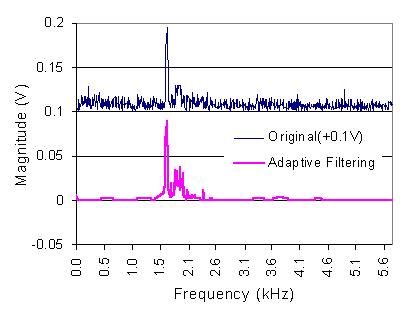
Fig. 4 Time function and spectrum of a seismic signal before and after
the adaptive filering
|